
With this new database, our users can expect 75% decrease in storage usage capacity on average. It also had some stability issues that resulted in taking up more device and iCloud storage. There are a number of reasons behind this decision, and they all came down to providing more reliability, privacy and long-term stability for our users.įor one, the pre-existing database didn't fully support the macOS ecosystem. With this release, we're also migrating to a brand-new and more reliable database. Without their ongoing feedback and encouragement, we would not have reached this point. On this huge milestone, we'd like to thank our loyal users who participated in our macOS (and iOS) beta programs. Sorted³ for macOS is also built with Apple Silicon support and macOS Big Sur widgets.
#Beta sorted3 mac
The following October, we decided to develop Sorted³ using Mac Catalyst as a more viable and long-term solution.
#Beta sorted3 for mac
After launching Sorted³, we shifted our focus back to a native Mac experience, before learning about iPad Apps for Mac (with code name Mac Catalyst) at WWDC 2019. This started with building a native Mac App back in 2016 (to complement the very first version of Sorted). Since the early days, we considered the Mac App to be an essential component of the overall Sorted experience.
#Beta sorted3 download
Our results indicate that simulation outcomes can lead to quite different conclusions, depending on the levels of multicollinearity and invariance of the betas used to generate the data.The much-anticipated Sorted³ for Mac is now available to download from the Mac App Store! The Mac App has been in the works for a while - We've gone through 3 product iterations to get to where we are today. Many previous studies have investigated the finite-sample properties of the TP estimators using the data generated with the estimated betas from actual data. Thus, we propose use of two pre-diagnostic statistics to measure these levels.

The levels of multicollinearity and invariance of betas can vary depending on the assets and sample periods used in estimation.
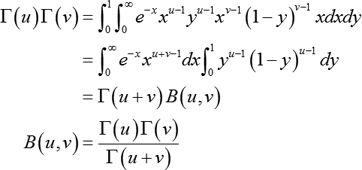
Second, the t-tests for hypotheses related to risk prices and pricing intercepts have only limited power. when data are generated by the betas with high levels of multicollinearity and invariance that can be observed from actual data. First, the TP estimators can have biases larger than 100% of true risk prices. Our simulation results show the following. This paper investigates the reliability of the two-pass (TP) estimators of factor risk prices when betas (multifactor loadings) have high levels of cross-sectional correlation (multicollinearity) and/or when some of them have small cross-sectional variations (near-invariance). Finally, we illustrate the functionality of our new procedures in an empirical application. We also highlight some limitations of current empirical practices and discuss what inferences can and cannot be drawn from returns to beta-sorted portfolios for either a single cross-section or across the whole sample. We study beta-sorted portfolios for both a single cross-section as well as for aggregation over time (e.g., the grand mean), offering conditions that ensure consistency and asymptotic normality along with new uniform inference procedures allowing for uncertainty quantification and testing of various relevant hypotheses in financial applications.

Our framework rationalize the well-known estimation algorithm with precise economic and statistical assumptions on the general data generating process and characterize its key features. We formally investigate the properties of beta-sorted portfolio returns by casting the procedure as a two-step nonparametric estimator with a nonparametric first step and a beta-adaptive portfolios construction.
Despite their widespread use, little is known of their statistical properties in contrast to comparable procedures such as two-pass regressions. Beta-sorted portfolios - portfolios comprised of assets with similar covariation to selected risk factors - are a popular tool in empirical finance to analyze models of (conditional) expected returns.


 0 kommentar(er)
0 kommentar(er)
